11488. Биномиальная
сумма
Дано натуральное число n. Найдите
значение следующей суммы
Вход. Одно натуральное число n
(n ≤ 30).
Выход. Выведите значение искомой суммы.
|
Пример
входа |
Пример
выхода |
|
3 |
20 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
Перепишем заданную сумму в виде:
![]() =
=
![]()
Сумма в скобках равна 2n. Если в формуле бинома Ньютона
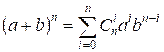
положить a = b = 1, то получим
соотношение:  , или
, или
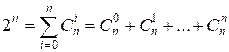
Вычислим
оставшуюся сумму:
![]() =
=
 =
=
 =
=
![]() =
= ![]()
Таким образом,
ответ равен 2n + ![]() =
= ![]() .
.
Пример
Вычислим ответ
для n = 3. При
непосредственном вычислении:
![]() =
= ![]() = 1 + 6 + 9 + 4 = 20
= 1 + 6 + 9 + 4 = 20
При вычислении
по формуле: ![]() = 20.
= 20.
Реализация алгоритма
Читаем входное значение n.
scanf("%lld", &n);
Вычисляем и выводим ответ.
res = (1LL <<
(n - 1)) * (n + 2);
printf("%lld\n", res);
Реализация алгоритма –
функция
Объявим массив для запоминания результатов: dp[n][k] =  .
.
int dp[31][31];
Функия Cnk
вычисляет значение биномиального коэффициента ![]() .
.
int Cnk(int n, int k)
{
if (n == k) return 1;
if (k == 0) return 1;
if (dp[n][k] != -1) return dp[n][k];
return dp[n][k] = (Cnk(n - 1, k - 1) + Cnk(n - 1, k)) % 9929;
}
Основная часть программы. Читаем
входное значение n.
scanf("%d", &n);
memset(dp,
-1, sizeof(dp));
Вычисляем указанную сумму.
res = 0;
for (i = 0; i <= n; i++)
res += (i + 1) * Cnk(n, i);
Выводим ответ.
printf("%d\n", res);
Python реализация – функция comb
import math
Читаем входное
значение n.
n = int(input())
Вычисляем указанную сумму. Для
вычисления биномиального коэффициента используем встроенную функцию comb.
res = 0
for i in range(n + 1):
res += (i + 1) * math.comb(n, i)
Выводим ответ.
print(res)
Python реализация – функция
Функия Cnk
вычисляет значение биномиального коэффициента ![]() .
.
def Cnk(n, k, dp):
if n == k: return 1
if k == 0: return
1
if dp[n][k] != -1: return
dp[n][k]
dp[n][k] = Cnk(n - 1, k - 1, dp) + Cnk(n - 1, k, dp)
return dp[n][k]
Основная часть программы. Читаем
входное значение n.
n = int(input())
Инициализируем все элементы двумерного списка dp
значением -1. Список используем для запоминания результатов: dp[n][k] =  .
.
dp = [[-1 for _ in range(31)] for _ in range(31)]
Вычисляем указанную сумму.
res = 0
for i in range(n + 1):
res += (i + 1) * Cnk(n, i, dp)
Выводим ответ.
print(res)
Python реализация – формула
Читаем входное
значение n.
n = int(input())
Вычисляем
ответ res по формуле.
res = (1 <<
(n - 1)) * (n + 2)
Выводим ответ.
print(res)